10 Multiple Choice Calc

1.

Find the particular solution to y ‘ = sin(x) given the general solution is y = C – cos(x) and the initial condition 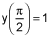. (5 points)

	-cos(x)
	2 – cos(x)
	-1 – cos(x)
	1 – cos(x)

2.

The slope of the tangent to a curve at any point (x, y) on the curve is 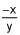. Find the equation of the curve if the point (2, -2) is on the curve. (5 points)

	x + y = 0
	x2 – y2 = -2
	x2 + y2 = 16
	x2 + y2 = 8

3.

The rate of decay in the mass, M, of a radioactive substance is given by the differential equation 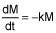, where k is a positive constant. If the initial mass was 100g, then find the expression for the mass, M, at any time t. (5 points)

	M = e-kt
	M = 100 e-kt
	M = 100 ekt
	M = 100ln(kt)

4.

The temperature of a pot of coffee varies according to Newton’s Law of Cooling: 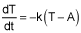, where T is the temperature of the coffee, A is the room temperature, and k is a positive constant. If the water cools from 90°C to 85°C in 1 minute at a room temperature of 30°C, find the temperature, to the nearest degree Celsius of the coffee after 4 minutes. (5 points)

	72
	42
	68
	81

5.

The differential equation 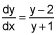(5 points)

I. produces a slope field with horizontal tangents at y = 2
II. produces a slope field with vertical tangents at y = -1
III. produces a slope field with columns of parallel segments

	I only
	II only
	I and II
	III only

6.

Which of the following differential equations is consistent with the following slope field?

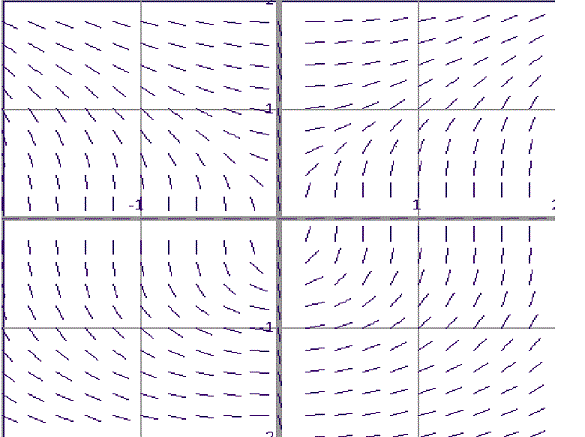(5 points)

7.

The general solution of the differential equation dy – 0.2x dx = 0 is a family of curves. These curves are all (5 points)

	lines
	hyperbolas
	parabolas
	ellipses

8.

Estimate the value of 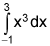by using the Trapezoidal Rule with n = 4. (5 points)

	8
	19
	22
	36

9.

The table below gives selected values for the function f(x). With 5 rectangles, using the midpoint of each rectangle to evaluate the height of each rectangle, estimate the value of 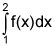. (5 points)

x	1	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9	2.0
f(x)	1	0.909	0.833	0.769	0.714	0.667	0.625	0.588	0.556	0.526	0.500

	0.7456
	0.6456
	0.6919
	0.6932

10.

Given f(x) > 0 with f ′(x) < 0, and f ′′(x) < 0 for all x in the interval [0, 1] with f(0) = 1 and f(1) = 0.3, the left, right, trapezoidal, and midpoint rule approximations were used to estimate 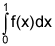. The estimates were 0.7915, 0.8405, 0.8410, 0.8421 and 0.8895, and the same number of subintervals were used in each case. Match the rule to its estimate. (5 points)

abcde	1.	trapezoidal
abcde	2.	right endpoint
abcde	3.	actual area
abcde	4.	midpoint
abcde	5.	left endpoint

a.	0.8895
b.	0.7915
c.	0.8421
d.	0.8405
e.	0.8410